Optimal Fair Contests

I show that any efficient two player symmetric allocation rule between risk neutral, heterogenous players generates weakly less revenue than one of two contests. The revenue maximizing efficient symmetric contest is an all-pay auction with bid caps (Che and Gale 1998) when heterogeneity is low and a difference form contest (Che and Gale 2000) when heterogeneity is high.

Introduction

Contests are models of conflict in which risk neutral players exert costly effort to win a prize. When one player is more capable than another, contests become less competitive. This lack of competitiveness decreases total effort. A contest designer can use two common tools to increase the total effort: reserve bids (Bertoletti 2016) and direct discrimination (Ewerhart 2017; Franke, Leininger, and Wasser 2018).

Reserve bids (i.e. inefficient allocation rules) allow the contest designer to require either player to exert some minimum amount of effort to qualify for the prize. A large enough reserve bid can make the lack of competition from a competitor irrelevant. For example, a professional figure skater would not need to exert much effort to beat me in a figure skating competition. However, if winning a large prize requires a high score, then the professional is not really competing against me. He is competing against this reserve bid. A large enough reserve bid can ensure any amount of individually rational effort.

Discrimination allows the contest designer to discriminate against the stronger player to reduce or remove her advantage. Handicaps in sporting events are a common example. This requires the contest designer to know which contestant is more talented. Otherwise, the designer does not know who to handicap. If this information is known, direct discrimination can be used to level the playing field of any contest.

We consider an alternative way of maximizing revenue – “fair” design. The contest designer maximizes the revenue of a contest under complete information without withholding the prize or treating contestants differently. We show that under these conditions, the designer is unable to achieve the first best and must give a positive payoff to the stronger player. However, allowing an arbitrarily reserve bid or direct discrimination ensures that the first best revenue can be achieved.

This work takes a similar approach to Letina, Liu, and Netzer (2020). However, unlike this work, I do not allow the principal to engage in direct discrimination or modify/withhold the prize. This work on optimal contest design contributes to a literature on revenue dominance in symmetric efficient contests (Fang 2002; Franke, Kanzow, Leininger, and Schwartz 2014) by characterizing an efficient symmetric contest which weakly dominates all others and contributes to a much larger literature on contest design.

Model

Suppose that the prize of contest is worth one to both players. So, the two players have the same value. However, their scores have different costs. In particular, we will say that the score is $k > 1$ times more costly for Player 2 than for Player 1. You can interpret this as saying that Player 1 is more skilled. So, it takes less effort for her to produce a high score.

The probability of Player $i$ winning the prize in a contest when she chooses score $s_i$ and her opponent chooses score $s_{-i}$ is:

$$p_{i}(s_i, s_{-i}).$$

The final payoffs are:

$$U_1(s_1, s_2) = p_1 (s_1, s_2) - s_1$$

$$U_2(s_1, s_2) = p_2 (s_2, s_1) - k s_2.$$

We define two notions of “fairness” that are central to our analysis:

• A contest satisfies efficiency iff $p_1 (x, y) + p_2 (y, x) = 1$ for all $x,y \geq 0$.
• A contest satisfies symmetry iff $p_1 (x, y) = p_2 (x, y)$ for all $x,y \geq 0$.

Efficiency means that someone is always a winner. Symmetry means that both players are treated the same by the designer. We will see that these conditions do not individually constrain the designer’s revenue. However, when the two conditions are imposed together, the designer is meaningfully constrained.

Note that these conditions jointly imply $p_i(x,x) = 0.5$.

Contest design

Suppose that there is some contest designer who can choose $p_1, p_2$ in order to maximize the expected revenue, $E[s_1 + s_2]$ given the (possibly mixed) strategies of the players. If strategies are pure, then the revenue is deterministic. Note that incentive compatibility implies

$$E[s_1 + k s_2] \leq E[p_1 (s_1, s_2) + p_2 (s_2, s_1)] \leq 1.$$

Therefore, expected revenue is bound above by $1 - (k - 1) E[s_2]$ and the first best is achieved iff $s_1 = 1$ and $s_2 = 0$.^[1] We can immediately see that no contest which satisfies both symmetry and efficiency will achieve the first best. This is because both players receive a payoff of zero in the first best, but Player 1 can choose zero instead of one to receive a payoff of $p(0,0) = 0.5$.

Reserve bid

If we allow for a reserve bid, but still enforce symmetry, is is easy for the designer to achieve the first best. For example, the following all-pay auction with a reserve bid achieves the first best:

$$p(x, y) = \begin{cases} 0 &\text{if } x < \max(y,1) \\ \frac{1}{2} &\text{if } x \geq 1, x=y \\ 1 &\text{if } x \geq 1, x > y. \end{cases}$$

This is because Player 1 is willing to meet the reserve bid of 1 and Player 2 is not.

One might wonder if the designer can still extract the full surplus with a smaller reserve bid. The answer is yes. In fact, $p(0,0) = 0$ is sufficient for the first best to be attainable under symmetry. That is, the designer need only be able to withhold the prize when both players play zero. To see this, consider the following contest which satisfies both properties except at zero.

$$p(x,y) = \begin{cases} 1 &\text{if } x-y >1 \\ x-y &\text{if } x-y \in(0,1] \\ 0 &\text{if } x = y = 0 \\ \frac{1}{2} &\text{if } x=y \neq 0 \\ 1+x-y &\text{if } x-y <0. \end{cases}$$

This contest has an equilibrium at the first best yet only denies the prize to players when they both exert no effort.

Direct discrimination

Direct discrimination is similar to a reserve bid. It is possible to mimic any reserve bid through direct discrimination by promising the prize to the weaker player whenever the reserve is not met. In particular, take either example from the previous section and set $p_1(x,y) = p(x,y)$ and $p_2(y,x) = 1 - p(x,y)$. Such a contest is efficient and will be strategically equivalent to the original contest. For example, consider the aforementioned all-pay auction with a reserve bid. With this transformation,

$$p_1(x, y) = \begin{cases} 0 &\text{if } x < \max(y,1) \\ \frac{1}{2} &\text{if } x \geq 1, x=y \\ 1 &\text{if } x \geq 1, x > y \end{cases}$$

$$p_2(x, y) = \begin{cases} 0 &\text{if } y \geq 1, y > x \\ \frac{1}{2} &\text{if } y \geq 1, x=y \\ 1 &\text{if } y < \max(x,1). \end{cases}$$

This contest has an equilibrium at the first best.

“Fair” design

We now restrict the principal to use an efficient symmetric contest. In equilibrium, each Player must weakly prefer her equilibrium payoff over copying the strategy of her opponent. Therefore, the following weak incentive compatibility condition is necessary for equilibrium:

$$\frac{1}{2} - E[s_2] \leq E[U_1(s_1, s_2)].$$

Together with $E[U_2(s_1, s_2)] \geq 0$ this implies

$$\begin{aligned} \frac{1}{2} - E[s_2] &\leq E[U_1(s_1, s_2) + U_2(s_1, s_2)] \\ \frac{1}{2} - E[s_2] &\leq 1 - E[s_1 + k s_2] \end{aligned}$$

where the last line follows from efficiency. Rearranging this equation gives an upper bound on the revenue:

$$E[s_1 + s_2] \leq \frac{1}{2} + (2 - k) E[s_2]$$

which can be further bounded by

$$E[s_1 + s_2] \leq \begin{cases} \frac{1}{k} &\text{if } k < 2 \\ \frac{1}{2} &\text{if } k \geq 2. \end{cases}$$

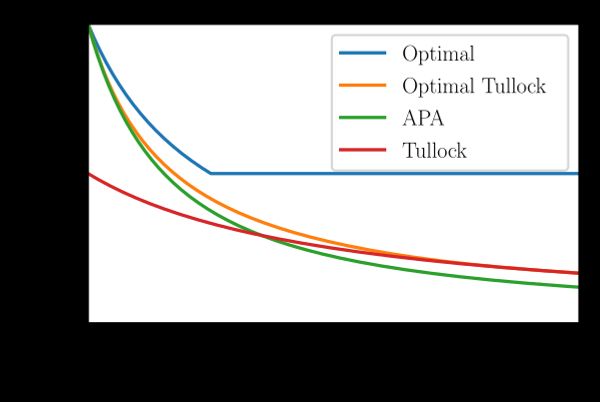
I show by construction that this upper bound is tight. That is, there exist optimal contests which achieve these bounds.

The second bound comes from the fact that $E[s_2] \leq \frac{1}{2k}$ because Player 2 cannot win with probability more than one half. To see this, consider that the following two conditions must hold in equilibrium

$$\begin{aligned} \frac{1}{2} - k E[s_1] &\leq E[p(s_2, s_1) - k s_2] \\ E[s_2] &\leq E[s_1] + (k)^{-1} \left(E[p(s_2, s_1)] - \frac{1}{2}\right) \end{aligned}$$

and

$$\begin{aligned} \frac{1}{2} - E[s_2] &\leq E[p(s_1, s_2) - s_1] \\ E[s_2] &\geq E[s_1] - \left(E[p(s_2, s_1)] - \frac{1}{2}\right) \end{aligned}$$

which imply $E[p(s_2, s_1)] \leq \frac{1}{2}$.

Case 1: $k < 2$. This means that revenue cannot exceed $\frac{1}{k}$. We can reach this upper bound with an all-pay auction with a bid cap at $\frac{1}{2k}$ as in Che and Gale (1998). That is

$$p(x,y) = \begin{cases} 1 &\text{if } \frac{1}{2k} \geq x > y \text{ or } y > \frac{1}{2k} \\ \frac{1}{2} &\text{if } x=y \\ 0 &\text{if } \frac{1}{2k} \geq y > x \text{ or } x > \frac{1}{2k}. \end{cases}$$

This has an equilibrium at $s_1 = s_2 = \frac{1}{2k}$ which achieves the upper bound for $k < 2$.

Case 2: $k \geq 2$. The above implies that revenue cannot exceed one half. Consider the following difference form contest as in Che and Gale (2000):

$$p(x,y) = \begin{cases} 1 &\text{if } x-y > \frac{1}{2} \\ \frac{1}{2} + x-y &\text{if } x-y \in \left[-\frac{1}{2},\frac{1}{2}\right] \\ 0 &\text{if } x-y < - \frac{1}{2} \end{cases}$$

The above contest has an equilibrium at $s_1 = \frac{1}{2}$ and $s_2 = 0$ which achieves the upper bound for $k \geq 2$.

---

---

1. Note that these strategies must be pure because no mixed strategy can have expectation zero and no individually rational mixed strategy can have expectation one. ↩︎